Question

What is the distance from point A to point Bto the nearest tenth of a foot?

Answer 1

From the given figure

Triangle ABC is the right angle triangle where C is the 90 degree

1)

Here we have θ=28, we need to calculate the Side of AB

Since AB is the hypotenuse of the triangle ABC and the side BC = 3ft, which is the base of the triangle ABC

Thus, apply the trignometric ratio of Cos

`\begin{gathered} \text{Cos}\theta=(Base)/(Hypotenuse) \\ \text{Cos (28)=}(BC)/(AB) \\ \text{Cos (28)=}(3)/(AB) \\ AB=(3)/(Cos(28)) \\ AB=(3)/(0.882) \\ AB=3.401\text{ f}eet \end{gathered}`

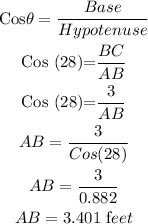
Answer : AB = 3.041 feet

2)

Here we have the string is stretched upto 5.2 feet i.e AB = 5.2 feet

We need to find the value of the angle,

thus again apply the trignometric ratio of Cos

`\begin{gathered} \text{Cos}\theta=(Base)/(Hypotenuse) \\ \text{Cos (}\theta\text{)=}(BC)/(AB) \\ \text{Cos (}\theta\text{)=}(3)/(5.2) \\ \text{Cos(}\theta)=0.576 \\ \theta=\cos ^(-1)(0.576) \\ \theta=54.83^(\circ) \end{gathered}`

So, the angle θ = 54.83

Answer : θ = 54.83

3)

when the θ=15 then the AB will be :

`\begin{gathered} \text{Cos}\theta=(Base)/(Hypotenuse) \\ \text{Cos (15)=}(BC)/(AB) \\ \text{Cos (15)=}(3)/(AB) \\ AB=\frac{3}{\text{Cos}(15)} \\ AB=(3)/(0.759) \\ AB=3.952 \end{gathered}`

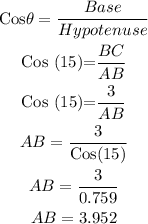
thus, at angle 15 the side AB = 3.1059 feet

Now, at an angle 30 the AB will be :

`\begin{gathered} \text{Cos}\theta=(Base)/(Hypotenuse) \\ \text{Cos (30)=}(BC)/(AB) \\ \text{Cos (30)=}(3)/(AB) \\ AB=\frac{3}{\text{Cos}(30)} \\ AB=(3)/(0.866) \\ AB=3.464\text{ f}eet \end{gathered}`

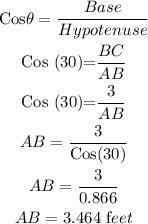
So, the collar will slide from point A to B when the angle changes from 15 to 30 is the difference between the side AB at 15 to AB at 30

Difference = 3.952 -3.464

Difference = 0.488 feet

Answer : 0.488 feet