Let me draw the figure here below:
Given that the measure of the angle CFE is 65°, we want to find the measure of the angle ACD.
First, notice that angle CFE and angle EFH are supplementary angles, so their sum is 180°:
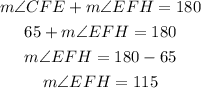
Now, there's a relation between angle EFH and angle ACD. Both angles are equal.
So, the measure of ACD is 115°.