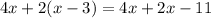
Part A:
Use distributive property on the left hand side:
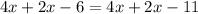
Add like terms:
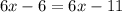
Add 6 to both sides:
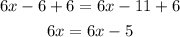
Subtract 6x from both sides:
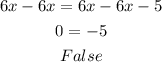
Therefore, the equation has no solution
Part B:
Addition Property of Equality
If two expressions are equal to each other, and you add the same value to both sides of the equation, the equation will remain equal.