Question

A single roller coaster car is at rest at the top of a hill of height h0 = 142 m. The cart rolls down over the track through points A, B, and C (with heights shown below). Find the coaster's speed at each of these points.hA = 17 mhB = 62 mhC = 122 mSpeed at point A = m/sSpeed at point B = m/sSpeed at point C = m/s

Answer 1

Given,

the heights,

h₀ =142 m

hA=17 m

hB=62 m

hC=122 m

When the roller coaster is at the top of the hill at rest, it will have maximum potential energy and minimum, that is zero, kinetic energy. As it rolls down, it gradually loses the potential energy and gains kinetic energy.

From the law of conservation of energy, the potential energy so lost will be equal to the kinetic energy gained by the cart at any given height.

That is,

`mg\Delta h=(1)/(2)mv^2`

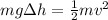
Where m is the mass of the cart and Δh is the difference in the height.

On rearranging the above equation,

`\begin{gathered} g\Delta h=(1)/(2)v^2 \\ \Rightarrow v=\sqrt[]{2g\Delta h} \end{gathered}`

Thus the speed at point A can be calculated as,

`v_A=\sqrt[]{2g(h_0-h_A)}`

On substituting the known values,

`\begin{gathered} v_A=\sqrt[]{2*9.8*(142-17)} \\ =\sqrt[]{2450} \\ =49.5\text{ m/s} \end{gathered}`

Thus the speed of the cart at point A will be 49.5 m/s

The speed of the cart at point B is,

`\begin{gathered} v_B=\sqrt[]{2g(h_0-h_B)} \\ =\sqrt[]{2*9.8*(142-62)} \\ =\sqrt[]{1568} \\ =39.6\text{ m/s} \end{gathered}`

Thus the speed of the cart at point B is 39.6 m/s

The speed of the cart at point C is,

`\begin{gathered} v_C=\sqrt[]{2g(h_0-h_C)} \\ =\sqrt[]{2*9.8*(142-122)} \\ =\sqrt[]{392} \\ =19.8\text{ m/s} \end{gathered}`

Therefore the speed of the cart at point C is 19.8 m/s