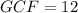By definition, a monomial is a polynomial that has one term.
In this case you have these monomials:
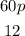
In order to find the Greatest Common Factor (GCF) of this pair of monomials (which is also known as Greatest Common Divisor), you can apply the steps shown below:
Step 1. You need to descompose each monomial into its prime factors, as following:
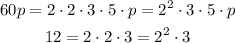
Step 2. Now you must choose the common factors with the lowest exponents and then you must multiply them. The product will be the Greatest Common Factor. Then:
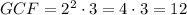
The answer is: