Given that the total length of the tape, d = 261 m
The time taken is
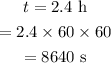
The linear speed will be
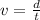
Substituting the values, the speed will be
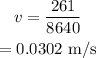
Also, the inner radius is
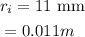
The outer radius is
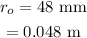
The radius will be
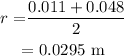
The angular speed will be given by the formula,
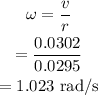
Thus, the common angular speed is 1.023 rad/s.