Picking any two points on the line on the Right Hand side of the graph, we have the following coordinates:
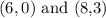
Finding the equation of the line with the coordinates above, we have::
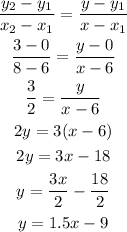
Picking any two points on the line on the left-hand side of the graph, we have the following coordinates:
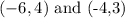
Finding the equation of the line with the coordinates above, we have::
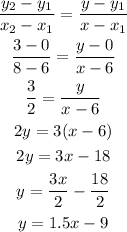
Hence, the piecewise function of the function; Y= 1.5x - 9 is