Given,
The mass of the fridge magnet, m=20 g
The force that is holding the fridge magnet, F=0.9 N
The coefficient of friction, μ_s=0.30
Where N is the normal force acting on the fridge magnet and f is the frictional force.
A.
The normal force acting on the fridge magnet is equal to the force that holds the fridge magnet to the surface of the fridge.
Thus the normal acting on fridge magnet is,

Thus the frictional force acting on the magnet is given by,

On substituting the known values,
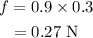
Thus the frictional force acting on the magnet is 0.27 N
B.
The weight of the magnet is given by,
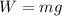
Where g is the acceleration due to gravity.
On substituting the known values,
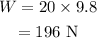
Thus the weight of the magnet is 196 N
C.
As the friction acting on the magnet is less than the weight of the magnet, the magnet will fall down.
The net vertical force acting on the magnet is given by,
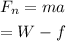
Where a is the acceleration of the magnet.
On substituting the known values,
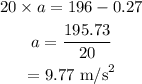
Thus the acceleration of the magnet is 9.77 m/s²