Question

Pls help with my algebra 2 hw!! I already have answers for a and b I just need c

Answer 1

The domain of the operation of two functions f and g is said to be the intersection of the individual domains, which is true for addition, subtraction, and multiplication of functions.

For the division of functions, an extra condition must be true: the denominator cannot be 0.

For example:

`\begin{gathered} f(x)=√(x) \\ g(x)=√(x-4) \end{gathered}`

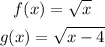
The domain of f is x ≥ 0 and the domain of g is x ≥ 4.

Note the intersection of the domains is x ≥ 4.

Now consider the function:

`h(x)=(f(x))/(g(x))=(√(x))/(√(x-4))`

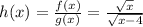
Here, we must exclude x = 4 from the domain of h because it would make the denominator 0, thus the domain of h(x) is x > 4 (excluding x = 4).

To find the range, we set x to a value real close to 4 (from the right side), like x = 4.001:

`h(x)=(√(4.001))/(√(4.001-4))=63.2`

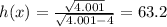
The value of h goes up as the values of x are closer to 4, thus the range has no limit to the right side.

Now give x a very high value like x = 100000:

`h(100000)=(√(100000))/(√(100000-4))=1.00002`

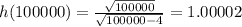
The value of h goes closer to 1 when x goes up to infinity. Thus the range is

(1, +∞).

In the following set of diagrams, Hanna's explanation is shown: