Question

4. Jacob bought some tickets to see his favorite group, and it cost $76. The relationship between the adult tickets, a, and the student's tickets, s, can be expressed by the equation 10a + 8C = 76. If he bought 4 adult ticket, then how student's tickets did he buy? If he bought 2 student ticket, then how adult's tickets did he buy? Which equation shows the number of student tickets as a function of the number of adult tickets? A. C= 68 – 10a B.C=76 – 10a C. C= -4/5a +38/5 D. C=-5/4a+19/2

Answer 1

Given the equation:

`10a+8c=76`

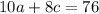
If Jacob bought 4 adult tickets, then a = 4, so we can solve for c:

`\begin{gathered} a=4 \\ \Rightarrow10(4)+8c=76 \\ \Rightarrow8c=76-40=36 \\ \Rightarrow c=(36)/(8)=(9)/(2)=4.5 \\ c=4.5 \end{gathered}`

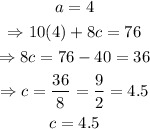
therefore, Jacob bought 4 or 5 students tickets.

Now, if Jacob bought 2 student tickets, then c=2 and for 'a' we have the following:

`\begin{gathered} c=2 \\ \Rightarrow10a+8(2)=76 \\ \Rightarrow10a=76-16=60 \\ \Rightarrow a=(60)/(10)=6 \\ a=6 \end{gathered}`

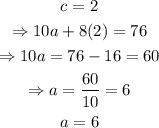
therefore, Jacob bought 6 adult tickets.

Finally, to find the equation that shows the number of student tickets as a function of adult tickets, we have to solve for 'c' to get the following:

`\begin{gathered} 10a+8c=76 \\ \Rightarrow8c=76-10a \\ \Rightarrow c=-(10)/(8)a+(76)/(8)=-(5)/(4)a+(19)/(2) \\ c=-(5)/(4)a+(19)/(2) \end{gathered}`

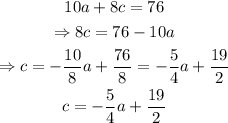
therefore, the function would be c = -5/4a +19/2