So,
Given the function:
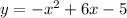
We're going to find the x-intercepts of the function as follows:
Step 1: Set the equation equal to zero.
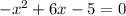
Step 2: We could multiply both sides of the equation by -1 so we could factor after that:

Now, we could factor this equation to solve for x and find the x-intercepts. To factor, we're going to find two numbers, whose sum gives us -6, and its product is 5. These numbers are -5 and -1, so we're going to group them in factors as follows:
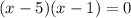
Solving for x, we notice that each factor could be zero, then:
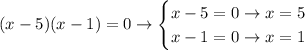
Therefore, the x-intercepts of the function are x=1 and x=5.
To find the vertex, we could use the fact that every quadratic equation of the form:

Has a vertex in the following coordinates:
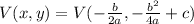
What we're going to do is to identify the values of a,b, and c (Which are the coefficients of the terms of the equation) and then replace them in the previous equation so we could calculate the coordinates of the vertex. This is,
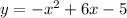
Where:
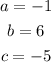
Replacing these values in the equation of the vertex, we got that:
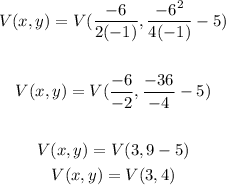
Therefore, the coordinates of the vertex are (3,4).