Question

The question is asking which tables of values represents an exponential Relationship but I wasn’t able to fit in the tables in one picture .I just need a brief explanation with the answer

Answer 1

Recall that an exponential relationship must always be expressed by one of the following:

1) an increasing function (that means that as x increases, the associated y-values also INCREASE)

or

2) a decreasing function (that means that as x increases, the associated y-values also DECREASE)

So as we look at the tables, a quick way to trim out all those that cannot be an exponential relationship is to see if any of them show an increasing and decreasing at the same time for example.

When you look at table A for example, you see that for the first three values of increasing x : -1, 0 , 1 the values for y go like: 4, 3, 4 (decreasing and then incresing. Therefore, we can discard this table. The data in table A is NOT exponential.

At the same time, recall that exponential functions are of the form:

`f(x)\text{ = a}\cdot b^x^{}`

which means that there is a factor "b" that is been multiplied every time as we increase in one unit .

Table B is not exponential either, since we see that for every increase in one unit in x, there is a constant increase in one unit for the y-value. So this is clearly a liner relationship and NOT exponential.

For table C: The first three pairs (x, y) represent a linear expression, with increase of one unite as x increases in one unit. then the function behaves differently. Then this is NOT and exponential expression.

Finally, Table D is the one that shows an exponential form. The

When x = 0 f(0) = 1 then we know that the parameter "a"is 1. then we know that when x = 1, f(1) = 2, which means that the form of the exponential relationship is:

`\begin{gathered} f(x)=a\cdot b^x \\ f(x)=1\cdot b^x \\ f(1)=1\cdot b^1 \\ 2=b \end{gathered}`

Then the factor that multiplies (base of the exponent) is "2".

That way we have all the numbers on the table covered with the expression:

`f(x)=1\cdot2^x`

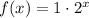
We can also add a graph of the plotted points that show an increasing exponential curve:

So please make sure you select the table D as the only exponential relationship of those listed in the four tables.