Question

The area of circle 1 is 6 square units. The area of circle 2 is 7 square units. Which of the following is true about the circumferences of the circles? A. The circumference of circle 1 equals the circumference of circle 2. B. Not enough information is given to make a comparison between the circumferences of the circles. C. The circumference of circle 1 is less than the circumference of circle 2. D. The circumference of circle 1 is greater than the circumference of circle 2.

Answer 1

The circumference of circle 1 is less than the circumference of circle 2.

Explanation:

Hi there!

When we compare two circles, if one is bigger than the other, it must have a greater circumference. We can see this visually.

If we want to prove this, we can take a look at the area and circumference formulas (r = radius):

`A=\pi r^2`

`C=2\pi r`

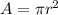
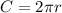
If we were to substitute the area formula into the formula for circumference, we would get the following:

`\displaystyle(A)/(\pi)=r^2\\\\\sqrt{\displaystyle(A)/(\pi)}=r`

`C=2\pi (\sqrt{\displaystyle(A)/(\pi)})`

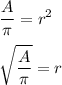
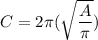
Therefore, the greater the area of a circle, the greater its circumference.

I hope this helps!

Answer 2

C. The circumference of circle 1 is less than the circumference of circle 2.

Explanation:

6<7

We know that the formula for the area of a circle is πr². This means the greater the radius, the greater the area.

We also know that the formula for circumference is 2πr. It is also dependent on radius. The greater the radius, the greater the circumference.

Given that Circle 2 has a greater area, this means that it has a greater radius which in turn means that it has a greater circumference.

C. The circumference of circle 1 is less than the circumference of circle 2.