Question

Find the coefficient of third term of (2x - 1)6.A.-240OB. 160OC. 240OD.-160Reset Selection

Answer 1

C. 240

Step-by-step explanation

We have to find the coefficient of the third term of (2x - 1)⁶. To do so, we have to find the expansion of this binomial, which is given by the Binomial Theorem Formula,

`(a+b)^n=\sum_(k=0)^n\binom{n}{k}a^(n-k)b^k`

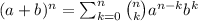
In this case, n = 6, a = 2x, and b = -1. The third term is when k = 2 - note that k starts with 0, so the third term in this case is,

`\binom{6}{2}(2x)^(6-2)(-1)^2=(6!)/(2!(6-2)!)\cdot(2x)^4\cdot1=(6\cdot5\cdot4!)/(2\cdot1\cdot4!)\cdot2^4x^4=(6\cdot5)/(2)\cdot16x^4=240x^4`

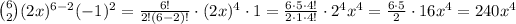
Hence, the coefficient of the third term is 240.