Question

I need help with this question for a b and c as I dont understand interest rate

Answer 1

a) The compound interest formula is, in general,

`A=P(1+(r)/(n))^(nt)`

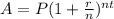
Where P is the initial amount, r is the interest rate, and n is the number of times the interest is compounded per unit t.

In our case,

`A=150000,n=12,r=0.105(=10.5\%),t=4`

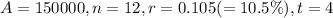
Thus, solving for P,

`\begin{gathered} \Rightarrow P=(A)/((1+(r)/(n))^(nt)) \\ \Rightarrow P=(150000)/((1+(0.105)/(12))^(12\cdot4)) \\ \Rightarrow P=98737.2365\ldots \end{gathered}`

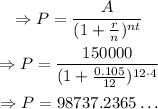
The answer to part a) is approximately $98737.24-> Interest + initial inversion equal to $150000

b)

We need to subtract P from Clem's inheritance, as shown below.

`250000-P\approx151262.76`

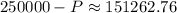
The answer to part b) is approximately $151262.76.

c)

Set P=250000 and solve for A as shown below.

`\begin{gathered} P=250000 \\ \Rightarrow A=250000(1+(0.105)/(12))^(12\cdot4) \\ \Rightarrow A=379795.924153\ldots \\ \Rightarrow A\approx379795.92 \\ \text{and} \\ I=A-P=379795.92-250000=129795.92\to\text{interest} \end{gathered}`

The answer to part c) is $129795.92-> Only interest