Let's make a diagram to visualize the problem.
As you can observe in the diagram above, the problem is asking for the angle between the 14-foot long wire and the ground. In order to find the angle, we have to use the law of cosines.
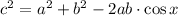
Where c = 17, a = 14, and b = 22. Let's replace these values and solve for x.
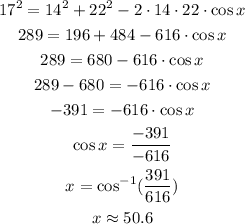
Therefore, the angle that the 14-foot long wire forms with the ground is 50.6°.