As we can see, both the pre-image and the image have the same orientation and are rotated the same. They differ on their positions and their sizes.
So, we will need at least one dilatation and we may need a translation too.
To figure out the factor of the dilatation, we can compare the corresponding side. The base, for instance, passed from 2 units on Figure A to 4 units on Figure B. This means that the dilatation factor is 4 over 2:
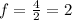
All options that hav dilatation have dilatation cnetered on the origin, so we will have to go with that.
To make a dilatation centered on the origin, we just apply the factor to all coordinates of the pre-image points.
The vertices of Figure A are (-1, -1), (-1, -4), (-3, -4) and (-3, -3).
Applying the factor of 2, we have:
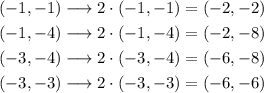
And the corresponding vertices of Figure B are (-2, 8), (-2, 2), (-6, 2) and (-6, 4).
Now, we need a translation to get from the dilated points to the points of Figure B. We can see thet the x-coordinates of the dilated points the the figure B are the same, -2, -2, -6 and -6, which means that we just need to translate it vertically.
We can take any corresponding pair of points as reference. For example, we can pick (-2, -2) and (-2, 8). That is, we want to translate from (-2, -2) to (-2, 8). To do this, we can translate 10 units up, which will add 10 units to each y coordinate. As we can see, applying this to all points should get us the vertices of Figure B:
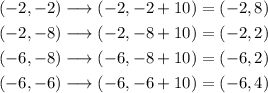
So, the correct options is the second option.
If the transformation maintain all the ratios of the figure, the pre-image and the image wioll be similar.
From rotation, reflection, translation and dilatation, the only one that can make them not similar is the dilation if they are done differently on the x and y directions. Since the dilatation we did was equal on both directions, it does not affect the similarity.
So, figure A and Figure B are similar.