Given,
The distance from the elbow joint to the point where the muscle is attached to the radial bone, d=3.6 cm=0.036 m
The mass of the forearm and the hand, M=2.7 kg
The combined length of the forearm and the hand, L=36 cm=0.36 cm
The mass of the ball. m=0.146 kg
From the diagram, the centre of mass of the forearm and the hand is at a distance of L/2.
For the arm to be in the rotational equilibrium, the net torque on the arm must be equal to zero.
That is,
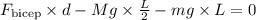
Where g is the acceleration due to gravity and F_bicep is the force applied by the bicep muscle.
On rearranging the above equation,

On substituting the known values,
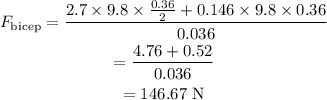
Thus the force that the bicep muscle must exert in order to keep the arm in rotational equilibrium is 146.67 N