Square base pyramid
We know that the volume of a square base pyramid is 144m³. And we know we can find it using the following equation:
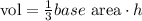
where h: height.
Since the base is a square, the area of the base is given by its width
area = w · w = w²
then, replacing in the first equation:
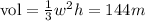
where w: width.
On the other hand, we have that its height, h, is twice its width, w:
2w = h
↓
w = h/2
Then, replacing w by h in our equation:
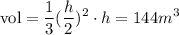
since the exponent is distributed to every part of the fraction we have:
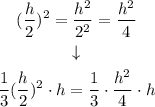
in order to operate them we can conver h into a fraction:
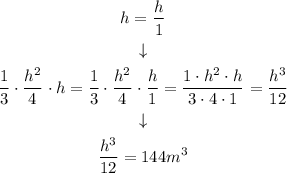
Now, we can solve the equation for h:
![\begin{gathered} \frac{h^3}{12^{}}=144m^3 \\ \downarrow \\ h^3=144m^3\cdot12=1728m^3 \\ \downarrow \\ h=\sqrt[3]{1728m^3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/af0kdljvdofnqujrksz3rzyt0k9dbj8wui.png)
We have that
![\sqrt[3]{1728m^3}=12m](https://img.qammunity.org/2023/formulas/mathematics/college/8wgysiyr21cgev6tzi0zwd0v2quskc70dj.png)
Then, h = 12 m (and w = 6m)
Answer: its height is 12m