Question

Ronald has a 12% solution of the fertilizer super grow. how much pure super grow should he add to the mixture to get 48 oz of a 17.5% concentration?

Answer 1

Note that a solution has two parts, one is called solute, and the other one is called solvent.

Here the solute is pure super grow fertilizer. And nothing is mentioned about solvent.

Let the mass of initial solution be 'x'.

Given the concentration of the solution initially is 12%,

So the mass of the pure super grow in the solution is 12%,

`m_i=(12)/(100)* x=0.12x`

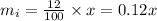
Thus, the mass of the solute in the initial solution is 0.12x, therefore the remaining mass 0.88x must correspond the solvent.

Now, consider the final solution. Given that the solution weighs 48 oz and has a concentration of 17.5%. So the mass of solute in the final solution is,

`m_f=(17.5)/(100)*48=8.4`

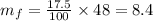
Thus, the mass of the solute in the final solution is 8.4 oz, therefore the remaining mass 39.6 oz must correspond the solvent.

Note that there is addition of pure super grow solution, but no addition of the solvent. So the mass of the solvent should remain conserved,

`0.88x=39.6\Rightarrow x=(39.6)/(0.88)=45`

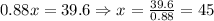
Thus, the weight of the initial solution 'x' is obtained as 45 oz.

Now, the amount of solute added is calculated by taking the difference between the amount of solutes in both the solutions,

`8.4-0.12x=8.4-0.12(45)=\text{8}.4-5.4=3`

Thus, Ronald should add 3 oz of pure super grow to get 48 oz of a 17.5% concentration.