SOLUTION
There will be 6 different orders in which the three people can finish first, second and third. Since, the race consists of three people then we are going to resolve the solution using permutation of the 3 people.
Therefore, we will have
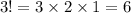
a) The different orders in which they can finish first, second and third are,
A B C
A C B
B A C
B C A
C A B
C B A
Yes, Harry is correct.
There will be 3 possible winners, only 2 possibilities for second place and only one person left for third place. This can be explained further using the permutation of the three people below,
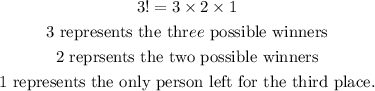
b) The number of ways people can finish in the following was will be,
i) 4-person race
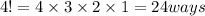
ii) 6-person race
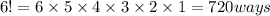
iii) 10-person race
