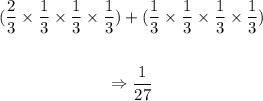Question

I require assistance with this: An infectious supervisor had meetings (contact) with 4 of his workers over the course ofthe day. If the probability of infection from a contact is 1/3, what is the probability that:i) None of the workers acquired the infection?ii) Exactly two workers acquired the infection?iii) More than 2 workers acquired the infection?

Answer 1

I) 16/81

II) 4/81

III) 1/27

Explanation:

We can think as each of the meetings as an independent event, as the probability of infection for each meeting does not depent on any other meeting and is never modified.

We have 4 seperate events independent events, and we have to analyze different combinations.

Part I:

Since the probability of infection is 1 out of 3, we can conclude that the probability that a coworker didn't get infected from the meeting is 2 out of 3, or

`(2)/(3)`

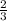
Therefore, the probability that none of the workers acquired the infection is:

`\begin{gathered} (2)/(3)*(2)/(3)*(2)/(3)*(2)/(3) \\ \\ \Rightarrow(16)/(81) \end{gathered}`

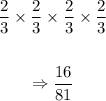
Part II:

Now we know that the probability of acquiring the infection is 1 out of 3 (1/3), and that the probability of not acquiring the infection is 2 out of 3 (2/3), we'll have that the probability that exactly two workers acquired the infection is:

`\begin{gathered} (2)/(3)*(2)/(3)*(1)/(3)*(1)/(3) \\ \\ \Rightarrow(4)/(81) \end{gathered}`

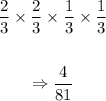
Part III:

To find the probability that more than 2 workers acquired the infection, we have to calculate the probability that exactly three workers acquired the infection and the probability that exactly four workers acquired the infection, and then add them up as folllowing:

`\begin{gathered} ((2)/(3)*(1)/(3)*(1)/(3)*(1)/(3))+((1)/(3)*(1)/(3)*(1)/(3)*(1)/(3)) \\ \\ \Rightarrow(1)/(27) \end{gathered}`