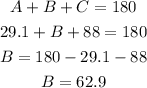Question

Given that ABC has m C = 88°, a = 12, and b = 22, find the remaining side length c and angles A and B, rounded to the nearest tenth.

Answer 1

We can solve this problem by using the law of cosines:

`c^2=a^2+b^2-2ab\cos C`

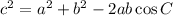
The given information is:

C=88

a=12

b=22

Then:

`\begin{gathered} c^2=12^2+22^2-2(12)(22)\cos 88 \\ c^2=144+484-528\cdot0.035 \\ c^2=144+484-18.43 \\ c^2=609.57 \\ c=\sqrt[]{609.57} \\ c=24.7 \end{gathered}`

Now, we can use the law of sines to find the other angles:

`(\sin A)/(a)=(\sin C)/(c)`

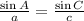
Replace the values and solve for A:

`\begin{gathered} \sin A=(a\sin C)/(c) \\ \sin A=(12\cdot\sin 88)/(24.7) \\ \sin A=(12)/(24.7) \\ \sin A=\text{0}.486 \\ A=\sin ^(-1)(0.486) \\ A=29.1 \end{gathered}`

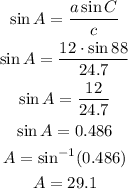
And the sum of the interior angles of a triangle is 180°, then:

`\begin{gathered} A+B+C=180\degree \\ 29.1\degree+B+88\degree=180\degree \\ B=180\degree-29.1\degree-88\degree \\ B=62.9\degree \end{gathered}`