Question

A tissue box is shaped like a right rectangular prism It has a base area of 16 square inches and a height of 5 1/3 inches. What is the volume of the tissue box? A. 21 1/3B. 26 2/3C. 42 2/3D. 85 1/3

Answer 1

D. 85 1/3

Step-by-step explanation

The volume of a right prism is the product of the area of the base, B, and the height of the prism, h,

`V=B\cdot h`

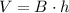
In this case, the base area is 16 in² and the height is 5 1/3 in,

`V=16in^2\cdot5(1)/(3)in`

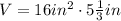
To multiply these two numbers, first, we have to convert the mixed number into an improper fraction by adding the whole and fraction parts,

`5(1)/(3)=5+(1)/(3)=(3\cdot5+1)/(3)=(15+1)/(3)=(16)/(3)`

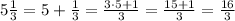
So the volume is,

`V=16\cdot(16)/(3)in^3=(16\cdot16)/(3)in^3=(256)/(3)in^3`

Now, we have to convert this improper fraction into a mixed number. To do so, we have to find the closest multiple of 3 that is less than 256. This number is 255, so we have to write the numerator as the sum of 255 and 1 to get 256,

`(256)/(3)=(255+1)/(3)`

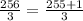
Distribute the denominator,

`(255+1)/(3)=(255)/(3)+(1)/(3)`

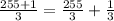
Simplify the first fraction,

`(255)/(3)+(1)/(3)=85+(1)/(3)`

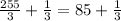
Hence, the volume of the box is 85 1/3 cubic inches