Question

The number of astronomy papers published increases by 3% every year. If 11,610 astronomy papers were published in a particular year, how many will be published 8 years later?If necessary, round your answer to the nearest whole number. astronomy papers

Answer 1

We are given that the number of papers increases by a percentage of 3% annually. since we have a quantity that grows by a percentage we can use the following exponential function:

`f(t)=a(1+r)^t`

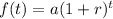
Where "r" is the rate of growth, "a" is the initial amount, and "t" is time. Replacing the values:

`f(t)=11610(1+0.03)^t`

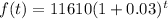
Simplifying:

`f(t)=11610(1.03)^t`

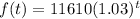
Now we replace t = 8:

`f(t)=11610(1.03)^8`

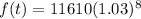
Solving the operations:

`f(t)=14707`

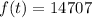
Therefore, 14707 papers will be published.