Question

The sunspot cycle (or solar magnetic activity cycle) is (nearly) periodic with a period of 11 years. Your goal is to make a simple model of the number of sunspots N(t) using a sine function. Specifically, the model has the form N(t) = Asin[B(t+C)] + D. To simplify the task, assume that: (1) the cycle is truly periodic with a period of 11 years; (2) the maximum number of sunspots Nmax on each cycle is always 300, and the minimum at each cycle is zero; (3) the number of sunspots at the initial time 0 is 0, that is N(t = 0) = 0. Write down the equation of your model (Provide a one line answer).

Answer 1

We have to find the parameters of the model:

`N(t)=A\sin[B(t+C)]+D`

where N is the number of sunspots and t is the time in years.

(1) The period is 11 years.

This affects the horizontal stretch of the function.

This can be related to the parameter B as:

`\begin{gathered} T=11 \\ (2\pi)/(B)=11 \\ B=(2\pi)/(11) \end{gathered}`

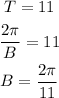
(2) The maximum number of spots is 300 and the minimum is 0.

This is related to the the parameters A and D, which control the vertical behaviour of the function.

The maximum number of spots happens when the sine function has a value of 1, so we can write:

`\begin{gathered} N_(max)=300 \\ A(1)+D=300 \\ A+D=300 \end{gathered}`

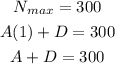
The minimum number of spots happens when the sine function has a value of -1.

We then can write:

`\begin{gathered} N_(min)=0 \\ A(-1)+D=0 \\ -A+D=0 \\ A=D \end{gathered}`

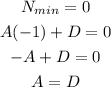
We then can find A and D as:

`\begin{gathered} A+D=300 \\ A+A=300 \\ 2A=300 \\ A=(300)/(2) \\ A=150 \\ D=A=150 \end{gathered}`

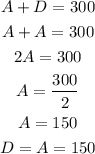
(3) The remaining parameter, C, will allow us to shift the phase the of the function.

We know that N(0) = 0.

This happens when the sine function is equal to -1.

Then, we can write:

`\begin{gathered} \sin[B(t+C)]=-1 \\ \sin[(2\pi)/(11)(0+C)]=-1 \\ (2\pi)/(11)(C)=(3)/(2)\pi \\ C=(11)/(2)\cdot(3)/(2) \\ C=(33)/(4) \end{gathered}`

We then can write the model as:

`N(t)=150\sin[(2\pi)/(11)(t+(33)/(4))]+150`

We can check the accuracy as:

Answer: N(t) = 150*sin(2π/11*(t+33/4))+150

A = 150, B = 2π/11, C = 33/4, D = 150