Question

A weightless beam supports a weight of 266N down. Find FA up at 3.00 m from this weight and FB up on the other side of this weight at 5.00m from it. Draw the situation.

Answer 1

The given problem can be exemplified using the following diagram:

To determine the value of the unknown force we will add the torques that act upon the point where the force F2 is acting. We will take torques that are clockwise to be negative and counterclockwise to be positive. Adding the torques we get:

`-(F_1)(3m+5m)+(266N)(5m)=0`

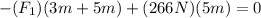
We set the sum equal to zero because we are assuming that the beam is in equilibrium.

Now, we solve the operations:

`-F_1(8m)+1330Nm=0`

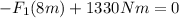
Now, we solve for the force, first by subtracting 1330 Nm from both sides:-

`-F_1(8m)=-1330Nm`

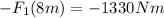
Now, we divide both sides by -8m:

`F_1=(-1330Nm)/(-8m)`

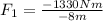
Solving the operations:

`F_1=166.25N`

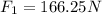
Therefore, the force that is 3 meters away from the weight is 166.25 Newtons. -

Now, to determine the force F2 we will add the forces in the vertical direction taking the forces downwards as negative and upwards as positive:

`F_1-266N+F_2=0`

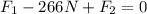
Now, we plug in the value of F2:

`166.25N-266N+F_2=0`

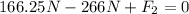
Solving the operations:

`-99.75N+F_2=0`

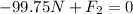
Now, we solve for F2 by adding 99.75N to both sides:

`F_2=99.75N`

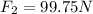
Therefore, the force that is 5 meters away must be 99.75 Newtons.