We are given the following equation
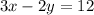
A. x-intercept
The x-intercept is the point where the line intersects the x-axis.
It can be found by substituting y = 0 into the equation.
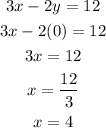
Therefore, the x-intercept is 4
x-intercept = (4, 0)
B. y-intercept
The y-intercept is the point where the line intersects the y-axis.
It can be found by substituting x = 0 into the equation.
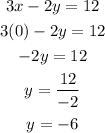
Therefore, the y-intercept is -6
y-intercept = (0, -6)
C. Slope
Recall that the slope-intercept form of an equation is given by

Where m is the slope and b is the y-intercept.
Let us convert the given equation into the above slope-intercept form.
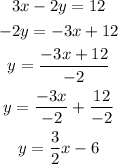
Comparing the above equation with the slope-intercept form, we see that the slope is 3/2
Slope = 3/2