Question

Hi. I need help, please. The problem is:The pressure exerted by a liquid on the bottom of a container is given by Ppg/ where "p" is the density of the liquid, "g" is the acceleration due to gravity (9.81 m/s), and "h" is the height of the container. liquid. What pressure is exerted on the bottom of a container containing mercury (p = 13.6 g/ml) if it reaches a height of 76.0 cm? Express your answer a) in Pascals and b) in atmospheres.

Answer 1

Given the formula for pressure:

`P=\rho gh`

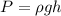
Where:

p = density

g = acceleration due to gravity

h is the height of the container.

Let's find the pressure exterted on the bottom of a container with the following:

p = 13.6 g/ml ==> 13600 kg/m³

g = 9.8 m/s²

h = 76.0 cm ==> 0.76 m

a) in Pascals.

Thus, we have:

`P=13600*9.81*0.76`

Solving further:

`P=101396.16\text{ Pa}`

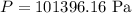
The pressure in Pascal is 101396.16 Pa.

(b) in atmospheres:

Where:

1 atm = 101325 pa

We have:

`(101396.16)/(101325)\text{atm}=1\text{ atm}`

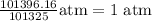
ANSWER:

(a). 101396.16 Pa

(b) 1 atm