To find the scale factor, let's first find the center of dilation. The dilation center, the vertice of the segment and its image, they all belong to the same line. If we call the center of dilation as O, we know that O, A, and A' are in the same line, and we can affirm the same for O, B, and B' . The center of dilation will be the interception of those two lines.
A and A' both belong to the line x = 6, B and B' both belong to the line y = -2.
This means, our center of dilation is (6, -2).
To find our scale factor, we can use the fact that Lengths of segments
|OA'| and |OA| relate to each other at the scale factor.
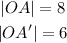
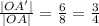
Our scale factor is 3/4.