Step 1:
Write the given data
![\begin{gathered} \operatorname{mean}\text{ }\mu\text{ = 82} \\ \text{Standard deviation = 4} \\ x\text{ betw}en\text{ 74 and 78} \end{gathered}]()
Step 2:
Write the z-score formula
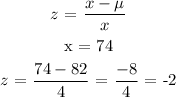

Step 3
Draw the normal curve
P(z=-2) = 0.02275
P(z=-1) = 0.15866
Step 4:
Probability that the score is between 74 and 78 = 0.15866 - 0.02275
= 0.13591
Percentage of students would expect to score between 74 and 78
= 0.135 X 100%
= 13.5%
Final answer
13.5%