Given the amount invested as 400 with an interest rate of 8%, the number of years it takes to reach 5,500 is calculated as
Thus,

Substituting the parameters in the equation, we have
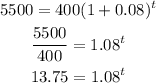
Taking the logarithm of both sides to base 10, we have
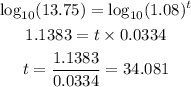
Thus, it will take 34.08 years (nearest hundredth) to reach 5,500.