Question

The shorter leg of a right triangle is 7 cm shorter than the longer leg. The hypotenuse is 7 cm longer than the longer leg. Find the side lengths of the triangle.Length of the shorter leg: ____cmLength of the longer leg: _____cmLength of the hypotenuse: _____cm

Answer 1

So,

Based in the information, we could draw:

Let "x" be the length of the longer leg.

We could find the dimentions of the triangle using the Pythagorean theorem:

`\begin{gathered} (x+7)^2=x^2+(x-7)^2 \\ x^2+14x+49=x^2+x^2-14x+49 \\ x^2+14x+49=2x^2-14x+49 \\ \to x^2-28x=0 \end{gathered}`

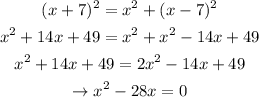
As you can see, we could solve this quadratic equation factoring:

`\begin{gathered} x^2-28x=0 \\ x(x-28)=0 \\ x=0\text{ or }x=28 \end{gathered}`

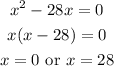
Note that the solution x=0 has not any sense in the context of the problem.

Therefore, the appropiate value of x is 28.

Now, we have found that the length of the longer leg is 28cm.

The shorter leg of the right triangle is 7 cm shorter than the longer leg, so its value is 21cm.

The hypotenuse is 7 cm longer than the longer leg, so, the value of the measure of the hypotenuse is 35cm.