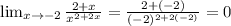Question

Calculus early transcendental functions. Does the limit exist?What’s the value of the limit?

Answer 1

To check if the limit exists, let's try inputting x = -2 (the lmiit) into the expression and see if it is defined:

`\begin{gathered} x=-2 \\ (2+\mleft(-2\mright))/((-2)^(2+2(-2)))=(2-2)/((-2)^(2-4))=(0)/((-2)^(-2))=0\cdot(-2)^2=0\cdot4=0 \end{gathered}`

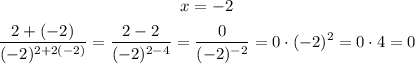
There is no problem with this reasoning, for example, there is no zero in the denominator or squaare root of a negative number, so the limit is the same as simply substituting x = -2.

So the answer is:

`\lim _(x\to-2)(2+x)/(x^(2+2x))=(2+(-2))/((-2)^(2+2(-2)))=0`