Question

What is the image point of (-6, -3) after the transformation R90 degrees r y=-x?

Answer 1

Given the point (-6, -3)

We will find the image of the point after the following transformation:

`R_(90)\circ r_(y=-x)`

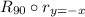
So, first, we will find the image of the reflection over the line y = -x and then apply the rotation of 90°

The rule of the reflection over the line y = -x will be as follows:

`(x,y)\to(y,-x)`

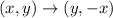
Apply to the given point:

`(-6,-3)\to(-3,6)`

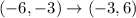
Then, we will find the result after the rotation of 90

the rule of the rotation will be as follows:

`(x,y)\to(-y,x)`

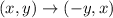
Apply to the point (-3, 6)

`(-3,6)\to(-6,-3)`

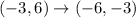
So, the answer will be (-6, -3)