First, let's determine the slope and y-intercept of the line to write the equation.
You can calculate the slope of the line using the formula:
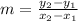
Where
(x₁,y₁) are coordinates of one of the points of the line
(x₂,y₂) are the coordinates of the second point
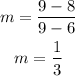
Using the point-slope form you can determine the equation of the line:
Use m=1/3 and (x₁,y₁) as (6,8)
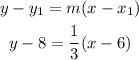
-distribute the multiplication on the parentheses term
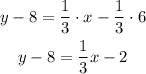
-add 8 to both sides of it
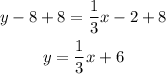
The y-intercept of the line is the constant of the equation b=6
Plot both points and link them to graph the line: