In this problem, we want to solve two inequalities.
There is one rule that is important to remember with inequalities:
- If you multiply or divide by a negative number in the last step, you must flip the inequality symbols.
We are given:
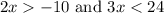
We can solve these one at a time. Beginning with the first inequality,
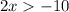
Divide by 2 on both sides:

Moving on to the second inequality, we get:

So now we know that x is greater than -5 but less than 8.
Let's see what that looks like on a numberline:
We see that the values of x can be included within a lower bound and an upper bound at -5 and 8.
This means we can write the final inequality as
[tex]\boxed{-5