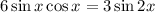Question

Use the sum and difference formulas or a double angle formula to rewrite theexpressions as sin, cos or tan(a) cos^2x - ½(b) 6 sin x cos x

Answer 1

We have the following trigonometric identities:

`\cos2x=2\cos\placeholder{⬚}^2x-1`
`\sin2x=2\sin x\cos x`

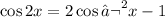
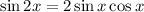
a)

From the first identity above we have that:

`\cos\placeholder{⬚}^2x=(\cos2x)/(2)+(1)/(2)`

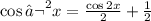
Plugging this in the expression given we have:

`\begin{gathered} \cos\placeholder{⬚}^2x-(1)/(2)=(\cos2x)/(2)+(1)/(2)-(1)/(2) \\ \cos\placeholder{⬚}^2x-(1)/(2)=(1)/(2)\cos2x \end{gathered}`

Therefore:

`\cos\placeholder{⬚}^2x-(1)/(2)=(1)/(2)\cos2x`

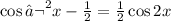
b)

From the second identity given at the beginning we have:

`\sin x\cos x=(1)/(2)\sin2x`

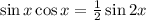
Plugging this in the second expression we have:

`\begin{gathered} 6\sin x\cos x=6((1)/(2)\sin2x) \\ 6\sin x\cos x=3\sin2x \end{gathered}`

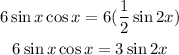
Therefore:

`6\sin x\cos x=3\sin2x`