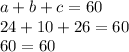Question

8. A right triangle has a perimeter of 60 cm. The legs have a ratio of 5:12. The hypotenuse is twice the

smallest leg increased by 6 meters. Find the length of a, b and c.

Answer 1

a=24

b=10

c=26

Explanation:

Perimeter is the sum of the sides (
`a+b+c=60`)

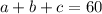The legs (a and b) have a ratio of 5:12, which means that
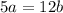`5a=12b`, which can be simplified to
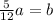`(5)/(12) a=b`, where b will be the smaller leg.

The hypotenuse will be double the smallest leg, 2b, increased by 6 meters, giving us an equation of
`c=2b+6`

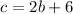
Let's plug these in to get one variable:

`a+b+c=60\\a+b+2b+6=60\\a+(5)/(12)a+2((5)/(12)a)+6=60\\(12)/(12)a+(5)/(12)a+(10)/(12)a+6=60\\(12)/(12)a+(5)/(12)a+(10)/(12)a=54\\(27a)/(12)=54\\27a=648\\a=24`

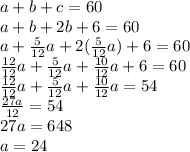
Now that we have a, we can plug it in to our previous equations to find our other sides:

`5a=12b\\5(24)=12b\\120=12b\\10=b`

`c=2b+6\\c=2(10)+6\\c=20+6\\c=26`

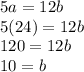
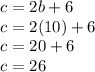
Double-checking:

`a+b+c=60\\24+10+26=60\\60=60`