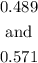Question

Hi, can you help me answer this question please, thank you!

Answer 1

We have the following data:

`\begin{gathered} n=560 \\ p=0.53 \end{gathered}`

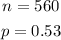
From the normal distribution curve, the z-score corresponding to 95% confidence interval to

95 % confidence interval, is 1.96

To construct the confidence interval, we will use the formula below

`\begin{gathered} p\pm z_{(\alpha)/(2)}\sqrt[]{(p(1-p))/(n)} \\ \text{where} \\ z_{(\alpha)/(2)}=1.96 \\ p=0.53 \\ n=560 \end{gathered}`

`\begin{gathered} 0.53\pm1.96\sqrt[]{(0.53(1-0.53))/(560)} \\ 0.53\pm1.96\sqrt[]{(0.53(0.47))/(560)} \\ 0.53\pm0.0413 \end{gathered}`

Thus the interval will be

`\begin{gathered} 0.53-0.0413=0.4887 \\ 0.53+0.0413=0.5713 \end{gathered}`

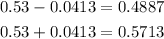
The values to 3 decimal places are

`\begin{gathered} 0.489 \\ \text{and} \\ 0.571 \end{gathered}`