Given:
a.) There were 598 tickets purchased for a major league baseball game.
b.) The general admission tickets cost $6.50.
c.) In the upper box, tickets cost $10.
d.) The total amount of money spent was $4,821.50
For us to be able to determine how many of each kind of ticket were purchased, let's first generate equations based on the given.
Let,
x = no. of general admission tickets
y = no. of upper box tickets
a.) There were 598 tickets purchased for a major league baseball game.
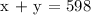
b.) The general admission tickets cost $6.50.
c.) In the upper box, tickets cost $10.
d.) The total amount of money spent was $4,821.50
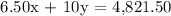
Substitute the 1st generated equation to the 2nd one and simplify.
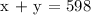
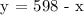
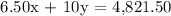
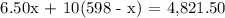
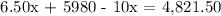
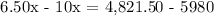
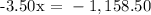
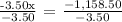

Therefore, 331 tickets of the general admission were purchased.
Let's determine the number of tickets purchased for the upper box.
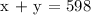
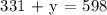
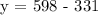
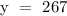
Therefore, 267 tickets of the upper box were purchased.
In Summary,
No. of general admission tickets sold = 331 tickets
No. of upper box tickets sold = 267 tickets