Mean:
![\begin{gathered} \bar{x}=(3.3+4.1+3.9+2.5+4.7+5.2+4.5+3.5+3.6+6.3+3.5+4.9+4.6+5.0+2.8+3.6+2.1+3.9+5.3+2.8)/(20) \\ \\ \bar{x}=4.005 \end{gathered}]()
Standard deviation:
![s=\sqrt[]{\frac{\Sigma(x_i-\bar{x})^2}{n-1}}](https://img.qammunity.org/2023/formulas/mathematics/college/2jdwu50mrmjzmgvvf0wcgbi3w5avow9htx.png)
Step by step:
1. Deviation: Subtract the mean from each data:
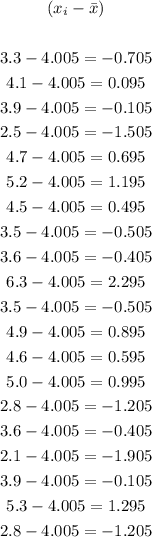
2. Square each deviation:
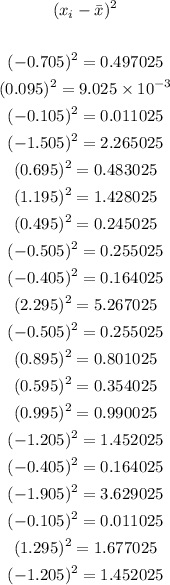
3. Add the square deviations:
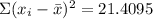
4. Divide the sum by one less than the number of data and take the square root of it to finally get the standard deviation:
![s=\sqrt[]{\frac{\Sigma(x_i-\bar{x})^2}{n-1}}=\sqrt{(21.4095)/(20-1)}=\sqrt{(21.4095)/(19)}=1.06](https://img.qammunity.org/2023/formulas/mathematics/college/fedco7lp0mrh8b4359tn9dq33inp6yc2v4.png)