Point-Slope Form of a Line
The equation of a line can be written in the so-called point-slope form as:
y = m(x - h) + k
Where m is the slope of the line and (h,k) is a point through which the line passes.
We need to determine the values of m, h, and k from the graph.
It can be seen the point (-3,1) belongs to the line, thus h = -3, k=1
To find the slope we need a second point. Though it's not directly given, we can take it from the graph. A clear point through which the line passes is (-2,-2).
The slope of a line can be calculated with the formula:

The coordinates of the points are (-3,1) and (-2,-2), thus:
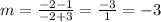
We now have the data needed to express the equation of the line:
y = -3 (x + 3) +1
It can also be expressed as:
y - 1 = -3( x + 3)