Question

Part B:Notice that two line segments are formed on each transversal between the central parallel line and the outer parallel lines. Measure the lengths of the four-line segments.Part CCalculate the ratio of the lengths of the two line segments formed on each transversal. You will have two sets of calculations. Round your answers to the hundredths place. What do you notice about the ratios of the lengths for each transversal? How do they compare?

Answer 1

To find the lengths of the four-line segments as you know the endpoints of each segment you use the next formula (formula to find the distance between two points):

`d=\sqrt{(x_2-x_1)\placeholder{⬚}^2+(y_2-y_1)\placeholder{⬚}^2}`

Segment KL:

`\begin{gathered} KL=\sqrt{(3-1)\placeholder{⬚}^2+(5.5-4.5)\placeholder{⬚}^2} \\ KL=√(2^2+1^2) \\ KL=√(4+1) \\ KL=√(5) \end{gathered}`

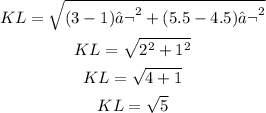
Segment LM:

`\begin{gathered} LM=\sqrt{(5-3)\placeholder{⬚}^2+(6.5-5.5)\placeholder{⬚}^2} \\ LM=√(2^2+1^2) \\ LM=√(4+1) \\ LM=√(5) \end{gathered}`

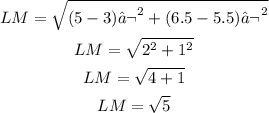
Segment PO:

`\begin{gathered} PO=\sqrt{(3-1)\placeholder{⬚}^2+(3-1.66)\placeholder{⬚}^2} \\ PO=√(2^2+1.34^2) \\ PO=√(4+1.7956) \\ PO=√(5.7986) \end{gathered}`

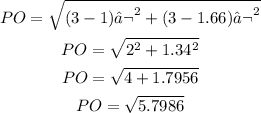
Segment ON:

`\begin{gathered} ON=\sqrt{(5-3)\placeholder{⬚}^2+(4.33-3)\placeholder{⬚}^2} \\ ON=√(2^2+1.33^2) \\ ON=√(4+1.7689) \\ ON=√(5.7689) \end{gathered}`

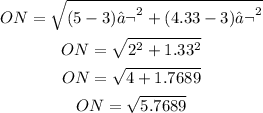
Part C:

The ratio of lengths of the two line segments formed on each transversal is the division of the lengths of the segments:

1st transversal: KL/LM

`(KL)/(LM)=(√(5))/(√(5))=1`

2nd transversal: PO/ON

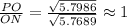
`(PO)/(ON)=(√(5.7986))/(√(5.7689))\approx1`The ratios are the same (1) in pair of segments in each transversal