Question

In a GEOMETRIC sequence, the first term is 21 andthe common ratio is 2. Find the 15th term.

Answer 1

From the question,

The geometric sequence has first term of 21 and common ratio of 2

hence

`\begin{gathered} first\text{ term, a = 21} \\ \text{common ratio, r = 2} \end{gathered}`

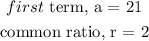
The general formula for nth term of a Geometric sequence is given as

`T_n=ar^(n-1)`

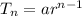
For the 15th term

The formula will be

`\begin{gathered} T_(15)=ar^(15-1) \\ T_(15)=ar^(14) \end{gathered}`

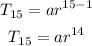
Applying the values of a and r

a = 21, r = 2

we have

`\begin{gathered} T_(15)=21(2)^(14) \\ T_(15)=21(16384) \\ T_(15)=344,064 \end{gathered}`

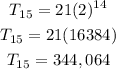
Therefore

The 15th term is 344,064