The final velocity of the player can be expressed as,
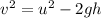
At the maximum height the final velocity of player is zero. Plug in the known values,
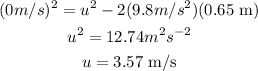
Now, when the initial velocity becomes, the final velocity of player as it moves. The final velocity can be expressed as,
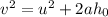
Substitute the known values,
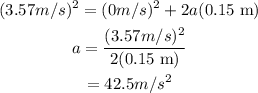
The jumping force of the player is,
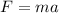
Substuting values,
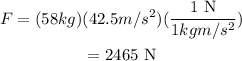
Thus, the jumping force acting on the player is 2465 N.