Question

The Math Club decides to sell t-shirts as a fundraiser to go to their next competition. They need to decide how much to charge for each t-shirt. A poll is taken and an estimate of the total number of t-shirts that the club can sell at different prices is provided in the table below. Price per t-shirt (in dollars) 5,10,12,15,20 Number of t-shirts sold 350, 250, 210, 150, 50 According to a linear model, approximately how many t-shirts could be sold for $8?

Answer 1

LGiven the table that shows the estimation of the total number of t-shirts that the club can sell at different prices (in dollars), you can identify the following points:

`(5,350),(10,250),(12,210),(15,150),(20,50)`

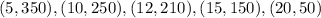
The equation of the line in Slope-Intercept Form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

You can find the slope using this formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where these points are two points on the line:

`(x_1,y_1),(x_2,y_2)`

In this case, you can substitute the coordinates of these points into the formula and evaluate, in order to find the slope of the line:

`(5,350),(20,50)`

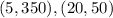
Then, you get:

`m=(50-350)/(20-5)=-20`

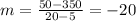
In order to find the value of "b", substitute the slope and the coordinates of one of the points into this equation:

`y=mx+b`

And solve for "b". Using the point:

`(20,50)`

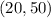
You get:

`50=-20(20)+b`
`\begin{gathered} 50+400=b \\ b=450 \end{gathered}`

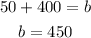
Now you know that the equation of this line in Slope-Intercept Form is:

`y=-20x+450`

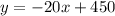
In order to find the approximate number of t-shirts that could be sold for $8, you need to substitute this value of "x" into the equation and evaluate:

`x=8`

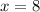
Then, you get:

`\begin{gathered} y=-20(8)+450 \\ y=290 \end{gathered}`

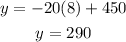
Hence, the answer is: Third option.