Question

Solve the system of equations.y=x^2-6y=-2x+9

Answer 1

The Solution.

The given system of equations is

`\begin{gathered} y=x^2-6\ldots eqn(1) \\ y=-2x+9\ldots eqn(2) \end{gathered}`

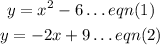
Equating both equations, we get

`x^2-6=-2x+9`
`\begin{gathered} x^2+2x-6-9=0 \\ x^2+2x-15=0 \end{gathered}`

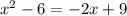
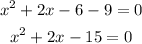
Solving the equation quadratically by Factorization Method.

We use 2x and - 5x to replace - 2x. we get

`x^2-3x+5x-15=0`

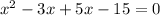
Factorizing, we get

`x(x-3)+5(x-3)=0_{}`
`\begin{gathered} (x+5)(x-3)=0 \\ x+5=0\text{ or x-3=0} \\ x=-5\text{ or x=3} \end{gathered}`

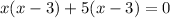
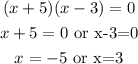
Substituting -5 for x, in eqn(2), we get

`\begin{gathered} y=-2x+9 \\ y=-2(-5)+9 \\ y=10+9=19 \\ (x=-5,y=19)\text{ or (-5,19)} \end{gathered}`

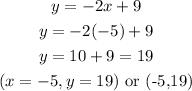
Substituting 3 for x, in eqn(2), we get

`\begin{gathered} y=-2(3)+9 \\ y=-6+9=3 \\ (x=3,y=3)\text{ or (3,3)} \end{gathered}`

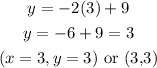
Hence, the correct answers are (-5,19) or (3,3)