Question

When a scientist conducted a genetics experiments with peas, one sample of offspring consisted of 919 peas, with 720 of them having red flowers. Ifwe assume, as the scientist did, that under these circumstances, there is a 3/4 probability that a pea will have a red flower, we would expect that689.25 (or about 689) of the peas would have red flowers, so the result of 720 peas with red flowers is more than expected.a. If the scientist's assumed probability is correct, find the probability of getting 720 or more peas with red flowers.b. Is 720 peas with red flowers significantly high?c. What do these results suggest about the scientist's assumption that 3/4 of peas will have red flowers?a. If the scientist's assumed probability is correct, the probability of getting 720 or more peas with red flowers is(Round to four decimal places as needed.)

Answer 1

a.

The sample is consisted of 919 peas and 720 have red flowers

If we assuma a 3/4 probavility that a pea will have a red flower, according to a binomial distribution (that is, which assumes only to possible outcomes: red and not red), the standard deviation must be given by:

`\begin{gathered} \sigma=\sqrt[]{np(1-p)} \\ \sigma=\sqrt[]{919\cdot(3)/(4)(1-(3)/(4))} \\ \sigma\approx\sqrt[]{172} \\ \sigma\approx13.1268 \end{gathered}`

Then, the Z score of 720 with a expected value of 689;25 and a standard deviation of 13.1268 is given by:

`Z=(720-689.25)/(13.1268)\approx2.3425`

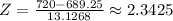
Using a normal approximation, according to a normal distribution table, we conclude that the probability of getting 720 or more peas with red flowers is given by 0.0096 = 0.96%

b.

Usually, when a