ANSWERS
(a) 3750 N
(b) 1.5 · 10⁶ N
(c) 400 times
Step-by-step explanation
(a) The force the seatbelt exerts on her is given by Newton's second law,
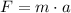
Rhonda's average acceleration is her speed divided by the brake time,

For this problem,
• m = 60.0 kg
,
• Δv = 25.0 m/s
,
• Δt = 0.400 s
![F=60.0\operatorname{kg}\cdot(25.0m/s)/(0.400s)=3750N]()
The average force exerted by the seatbelt on Rhonda is 3750 N.
(b) The same principle applies in this case. This time, Δt = 1.0 · 10⁻³ s, instead of 0.4s as before,
![F=60.0\operatorname{kg}\cdot(25.0m/s)/(0.001s)=1500000N=1.5*10^6N]()
The force the windshield exerted on her was 1.5 · 10⁶ N.
(c) To find how many times greater the stopping force of the windshield is than the seatbelt, we have to divide the force found in part b by the force found in part a,
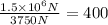
The stopping force of the windshield is 400 times greater than the seatbelt force.